Small objects can have tremendously different properties than their macroscopic counterparts. This also applies to crystals. Fore examples, shrinking a gold crystal to the micron or nanometer scale can make it more than ten times stronger. The origin of this size-affected strength has been one of the questions in our research program. Below you find some highlights around this topic, and you are also invited to explore how we used micro-Laue diffraction to trace the deformation of microcrystals.
Plasticity of dislocation free crystals
How strong is a dislocation free fcc metal? Do dislocation free fcc structures show a size-effect in strength? These questions have motivated to extract Ni3Al (L12, fcc) nanocubes from a commercially available superalloy. The extracted pristine nanocubes where mechanically tested
and show strengths up to G/17 that exceed 10 GPa. A slight exposure of a Ga-beam with an equivalent dose of 0.44 ions/nm2 reduces not only the highest achievable strength by more than 50% of the mean, but also changes the stress-strain response dramatically: pristine nanocubes collapse fully once reaching a critical stress, whereas irradiated nanocubes show strain hardening. Varying the cube size also suggests that the underlying dislocation nucleation processes, which facilitate plasticity in the priste cubes, is to some extent size-dependent. This project was done in collaboration with Prof. Sammy Tin and Dr. Bin Gan from IIT in Chicago. Read our publication in Small to find out more!
Selected publications:
Ultrahigh Strength of Dislocation-Free Ni3Al Nanocubes
How to explain the size-effect in strength?
Summarizing a large quantity of data exhibiting strenght-size scaling, one naturally has to ask the question if there is a mechanistic origin to this impressive power-law trend or nor? Peters and my viewpoint is that there should be a much more fundamental origin to this size-effect considering the large number of underlying microstructures present in the data. With this basic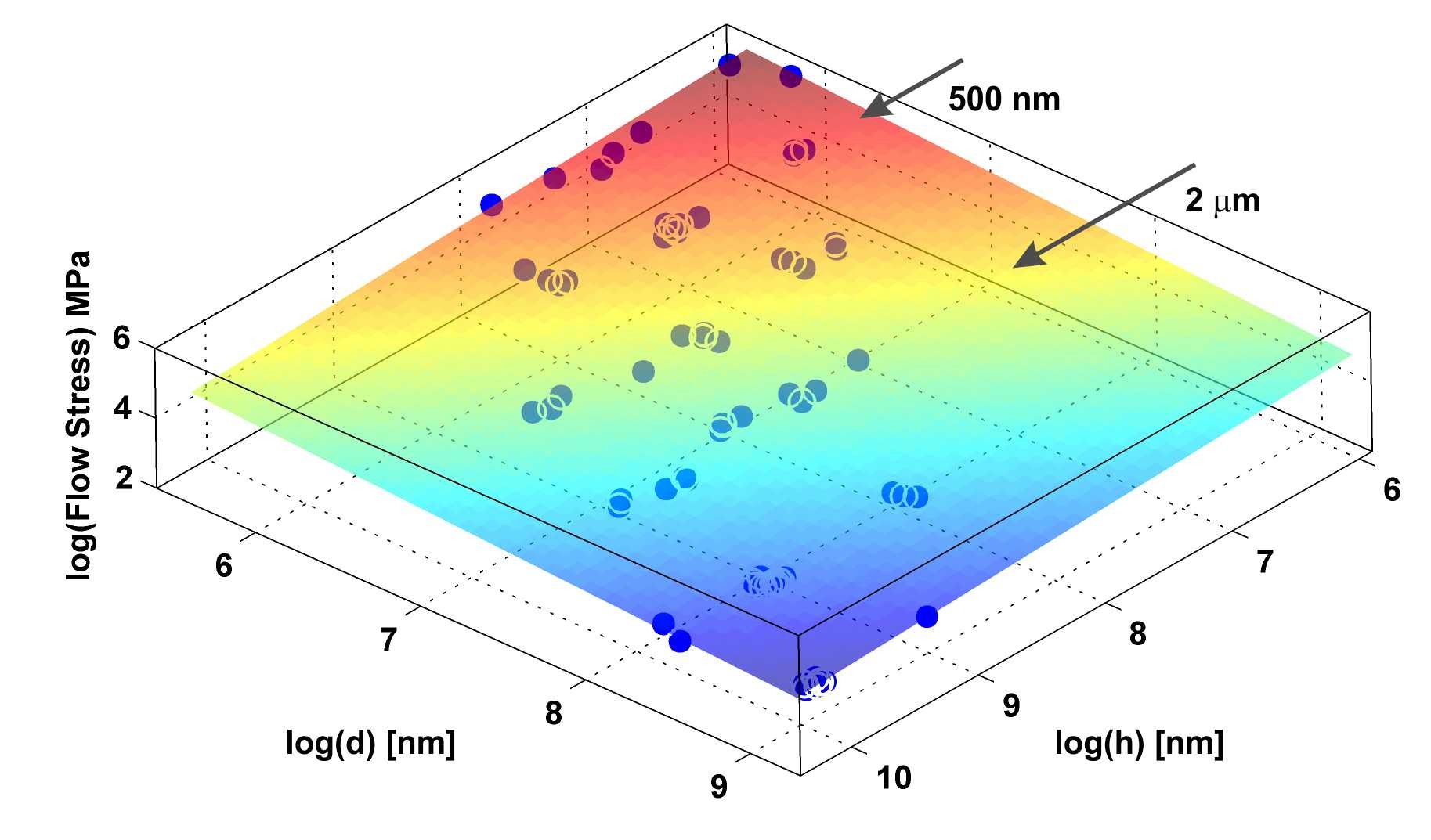 
approach, the size-effect can indeed be derived analytically with assuming a generic critical stress distribution and the fact that dislocation networks exhibit scale free behavior. This work predicts the experimental power-law exponent, which is only dependent on two parameters: one that characterizes the statistical extreme value regime of the underlying distribution, and a second that is the scaling exponent for intermittent dislocation plasticity. In addition to the model development (Phil. Mag.), we have successfully tested the stress-scaling prediction of the model with experiments (Scripta Mater.). This work clearly shows how the scaling exponent for size-strengthening is linked to the crystals critical stress distribution.
Selected publications:
A probabilistic explanation for the size effect in crystal plasticity
Crystal size effect in two dimensions – Influence of size and shape